Principio de Certeza Máxima

Introducción: ¿puede un sistema aleatorio conservar información?

En física, las leyes de conservación —como las de la energía o la cantidad de movimiento— son fundamentales para explicar el comportamiento de los sistemas. En el campo probabilístico, sin embargo, la existencia de un principio análogo que preserve alguna magnitud no había sido claramente formulada. El presente trabajo propone un avance conceptual y metodológico: el Principio de Certeza Máxima (PCM), una nueva invariante probabilística aplicable a fenómenos naturales de comportamiento aparentemente aleatorio, como las tormentas de lluvia.

Inspirado en el principio de mínima acción de la mecánica clásica, el PCM se desarrolla a partir de la conservación de la información que recibe y entrega un sistema probabilístico. Esta formulación se prueba en el caso de la distribución exponencial truncada y se generaliza a otras funciones de densidad, proponiendo una herramienta de modelación rigurosa para eventos naturales con estructura temporal.

Fundamentos teóricos: del funcional al equilibrio probabilístico

El PCM se construye a partir de un funcional denominado Funcional de Certeza, que actúa como una cantidad invariante en el tiempo. Este funcional se maximiza utilizando el cálculo variacional, de forma análoga al tratamiento determinista del principio de mínima acción. Su solución, bajo ciertas condiciones, conduce a una distribución de probabilidad que representa el arreglo temporal más probable entre todos los posibles.

El concepto se formaliza en torno al equilibrio entre dos funciones fundamentales:

• Conocimiento (C): información acumulada por el sistema, que combina experiencia y creencia.

• Información (I): cantidad de datos nuevos que el sistema recibe al ocurrir un evento aleatorio.

Cuando un evento ocurre, se dice que el sistema está en equilibrio probabilístico si la suma de la información recibida y la entregada se mantiene constante. Esta condición lleva a que la Certeza sea una cantidad invariante.

Aplicación a la distribución exponencial truncada

La distribución exponencial truncada sirve como caso de estudio para demostrar el principio. En particular, se analiza cómo el orden de aparición de eventos dentro de un intervalo de tiempo finito puede modelarse como una sucesión sin reemplazo, reflejando comportamientos disipativos comunes en la naturaleza.

Este modelo es capaz de capturar fenómenos “tempranamente intensos”, como:

• Tormentas de lluvia

• Terremotos

• Deslizamientos

El análisis discreto muestra que ciertos arreglos temporales (como aquel en el que los eventos más intensos se presentan al inicio) son estadísticamente más probables. La probabilidad de cada permutación puede calcularse a partir del funcional de certeza.

Figura 1. a) Certeza Máxima b) Certeza Mínima.
Comparación entre los escenarios de mayor y menor probabilidad en el tiempo. La Certeza Máxima representa el comportamiento más recurrente dentro del conjunto de trayectorias posibles.

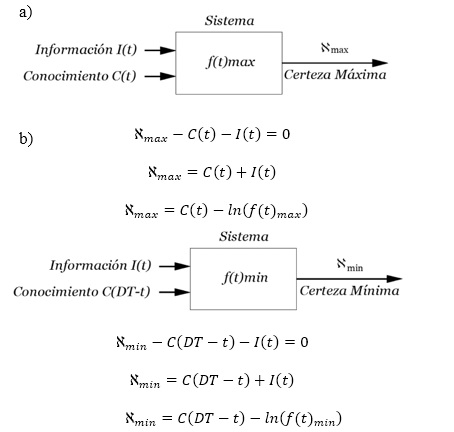
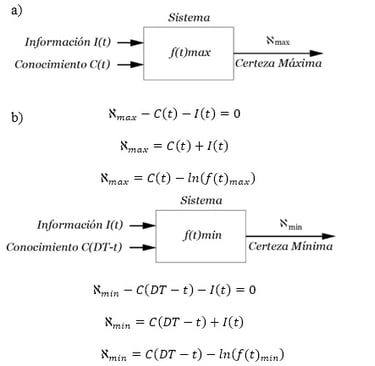
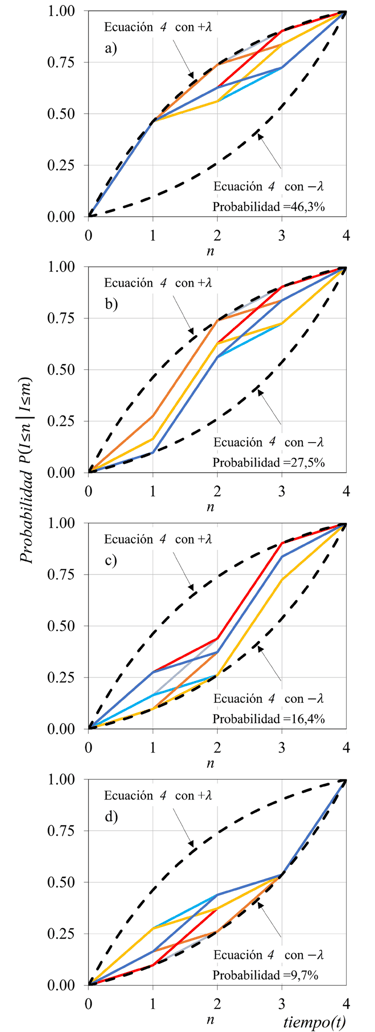
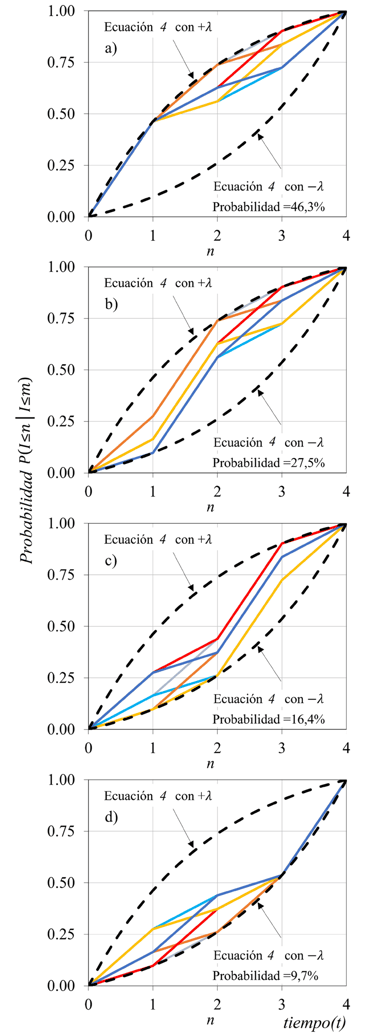
Figura 2. Patrones Temporales Exponenciales Truncados

Generalización: del caso exponencial a otras distribuciones

El principio no se limita a la distribución exponencial truncada. Utilizando funciones de conocimiento adecuadas, el PCM puede derivar otras funciones de densidad conocidas como:

• Uniforme

• Normal (truncada y no truncada)

• Weibull

• Erlang

• Gamma

Cada distribución presenta una certeza máxima asociada que puede utilizarse como criterio para seleccionar la función más adecuada para modelar un fenómeno natural dado.

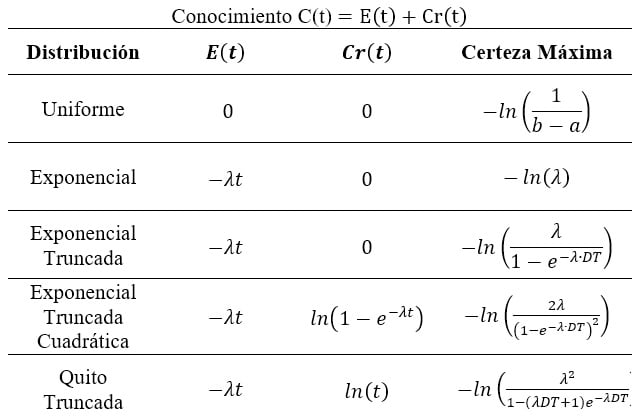
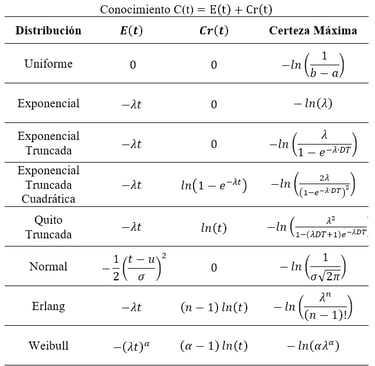
Figura 3. Conocimiento C(t) y Certeza Máxima asociadas a diferentes distribuciones

Caso de estudio: tormentas en el Distrito Metropolitano de Quito

El principio fue aplicado en la modelación espacio-temporal de tormentas sobre un área de 1600 km² en Quito, Ecuador. Se utilizó una combinación de distribuciones Weibull (para precipitación máxima) y exponencial truncada cuadrática (para duración temporal), con un parámetro α calibrado en 9,8 (coincidente con la gravedad terrestre en Quito).

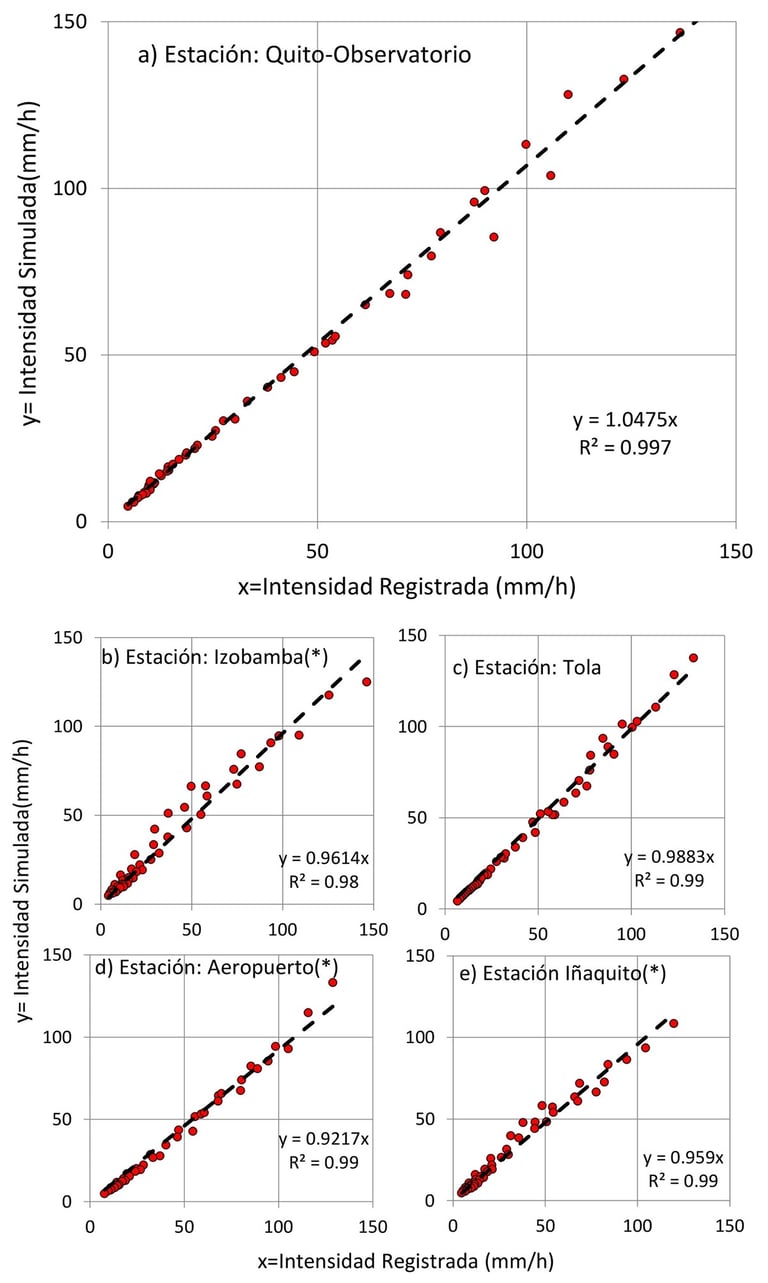
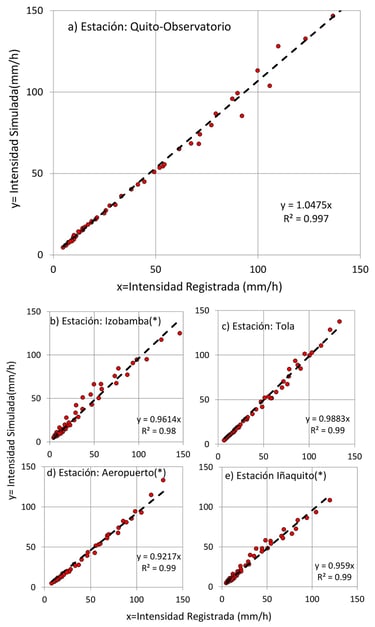
El modelo MIT-Q fue validado con datos de cinco estaciones meteorológicas, comparando las simulaciones con las curvas oficiales IDF de la Empresa Pública Metropolitana de Agua Potable y Saneamiento (EPMAPS).

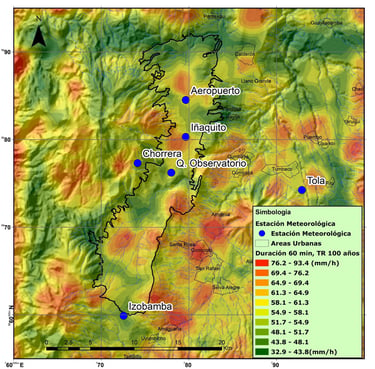
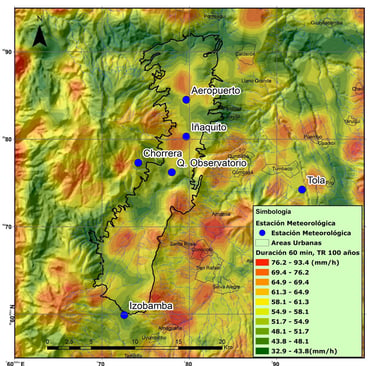
Figura 4. Figura 8. Intensidad de lluvias extrema Tr = 100 años, duración 1 hora.

Figura 5. Calibración y validación del modelo MIT-Q en distintas estaciones meteorológicas.

Conclusiones

El Principio de Certeza Máxima propone una nueva manera de comprender y modelar fenómenos naturales en el dominio probabilístico. A partir del equilibrio entre conocimiento e información, se define una cantidad invariante que permite derivar funciones de densidad óptimas bajo condiciones específicas.

Este enfoque:

• Introduce un marco teórico análogo al principio de mínima acción.

• Generaliza el uso de distribuciones probabilísticas con sentido físico.

• Demuestra su aplicabilidad en la simulación estocástica de tormentas.

• Ofrece una alternativa conceptual a la teoría clásica de la entropía.

La formulación del PCM representa un paso adelante hacia una ingeniería probabilística más profunda, que escucha a los fenómenos naturales y responde con ciencia.